AStar

搜索部分简介

Dijkstra 戴克斯特拉算法（广度优先）

戴克斯特拉算法 - 维基百科，自由的百科全书

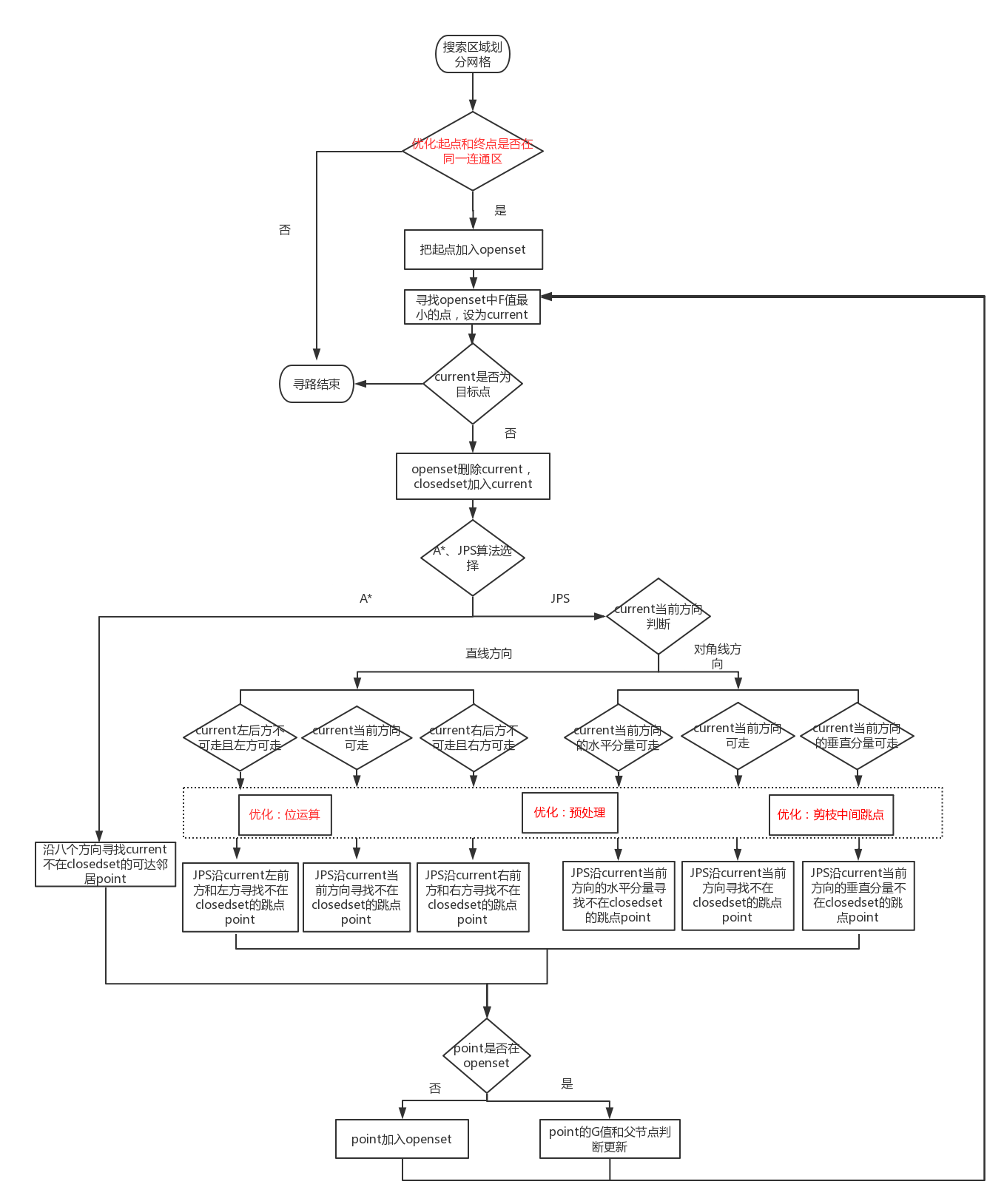
JPS算法

跳点搜索算法JPS及其优化

跳点搜索算法 (JPS算法) && 效率优化(摘录)

AStar

用简单直白的方式讲解A星寻路算法原理 - 立航 - 博客园

F = G + H

F - 方块的总移动代价

G - 开始点到当前方块的移动代价

H - 当前方块到结束点的预估移动代价

G值 = 父节点的G值 + 父节点到当前点的移动代价

H值 = 当前点到结束点的曼哈顿距离（优化点）

伪码：

• a、将开始点记录为当前点P
• b、将当前点P放入封闭列表
• c、搜寻点 P所有邻近点，假如某邻近点既没有在开放列表或封闭列表里面，则计算出该邻近点的F值，并设父节点为P，然后将其放入开放列表
• d、判断开放列表是否已经空了，如果没有说明在达到结束点前已经找完了所有可能的路径点，寻路失败，算法结束；否则继续。
• e、从开放列表拿出一个F值最小的点，作为寻路路径的下一步。（优化点）
• f、判断该点是否为结束点，如果是，则寻路成功，算法结束； 否则继续。
• g、将该点设为当前点P，跳回步骤c。

使用

var finder = new AstarPathFinder(map, Heuristic2D.Manhattan, new Neighours2D() {AllowDiagonal = false}
							,map,new DefaultCostSniffer());

PUtil.PreBakeWalkableAndCost(finder, map, null);
finder.GetPath(req, (result) => {
								 Debug.Log(result.nodes.Count());
            }, result => { Debug.LogError("Not Found"); });

拓展G值（不同的物体、到达不同方块的G值权重不同。坦克、飞机、湖泊）

根据合适的方式估算H值（曼哈顿距离进行预估：H = 当前方块到结束点的水平距离 + 垂直距离）

开放列表

• 用于记录所有可考虑选择的格子

封闭列表

• 用于记录所有不再考虑的格子

优化

• 得出路径后，对路径进行平滑处理
• 选择排序更快的二叉树来作为开放列表，帮助我们更快地从开放列表中取出F值最小的点；
• 采用布兰森汉姆算法预先判断两点是否可以直接通行，可通行就直接返回两点的直线路径，不可直接通行再采用A星算法寻路，提高寻路效率。

跳点搜索